欧拉角 、四元数、万向锁
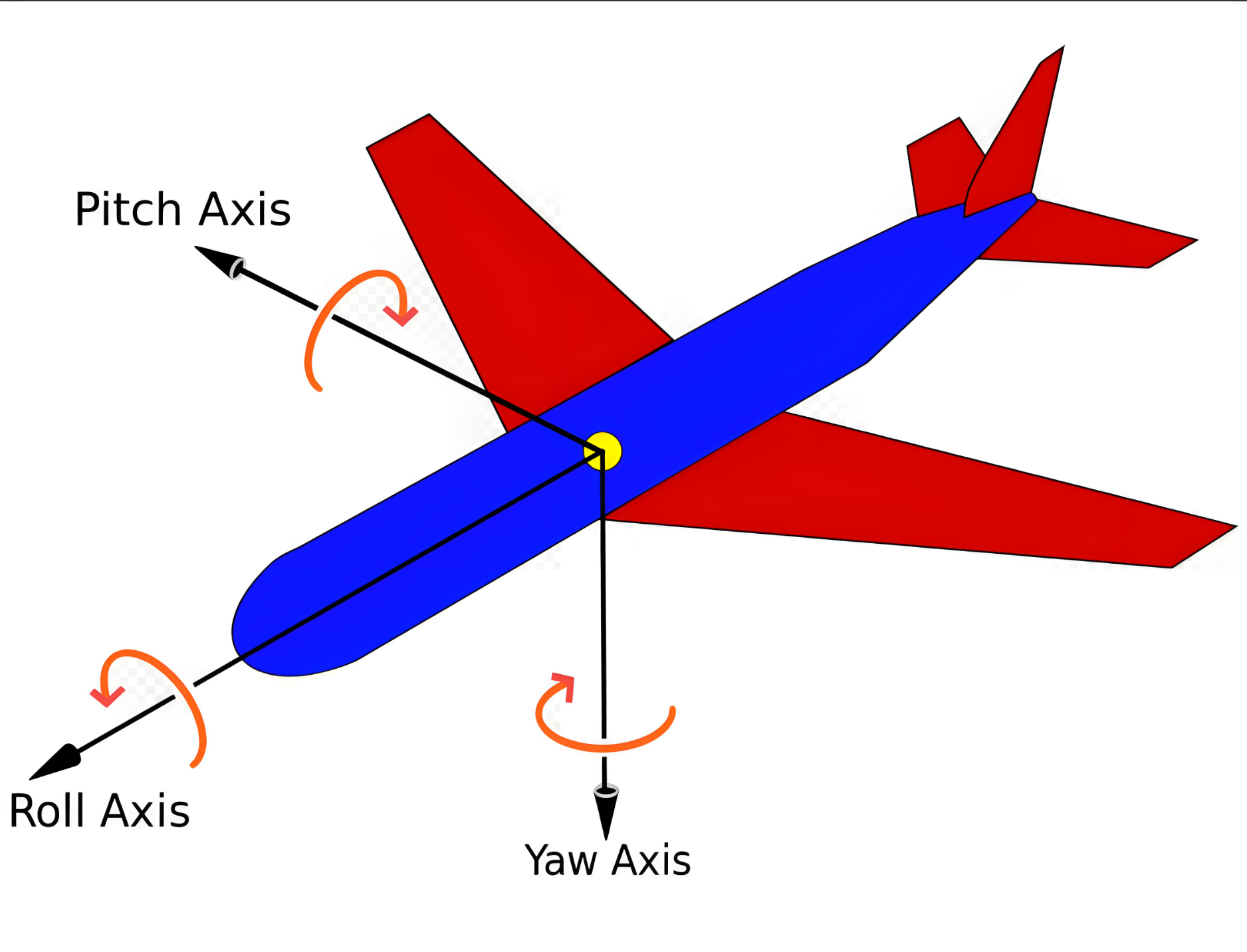
如果问一个普通人:“如何描述一架飞机在空中翻转的姿态?” 他可能会说:“机头抬起来(俯仰)、向左转(偏航)、再翻个跟头(滚转)。” 这种用三个独立旋转角度描述姿态的方式,就是欧拉角(Euler Angles)的由来。

一、欧拉角
欧拉角的核心思想是:用三个绕固定轴(或物体自身轴)的旋转角度,组合出任意3D姿态。它的命名源于瑞士数学家莱昂哈德·欧拉(Leonhard Euler),他证明了“任何3D旋转都可以分解为三个轴的旋转”。
最常见的欧拉角顺序是ZYX(对应飞机的“偏航-俯仰-滚转”):
绕Z轴旋转(偏航,Yaw):机头左右摆动(如“左转30度”);
绕Y轴旋转(俯仰,Pitch):机头上下摆动(如“抬头45度”);
绕X轴旋转(滚转/横滚,Roll):机身左右翻转(如“向左翻滚60度”)。
这种分解方式完全符合人类的直觉——我们从小到大接触的“转身”“抬头”“翻跟头”,本质上都是这三个动作的组合。因此,欧拉角在输入(如游戏手柄控制角色转向)和显示(如调试界面显示姿态角)中广受欢迎。
小tips:航模遥控中的美国手就是:左手摇杆上下控制油门、左右控制偏航,右手上下控制俯仰 、左右控制横滚
日本手就是:左手上下控制俯仰 、左右控制横滚,右手摇杆上下控制油门、左右控制偏航
2. 欧拉角的“阿喀琉斯之踵”:万向锁
但欧拉角有一个致命缺陷——万向锁(Gimbal Lock)。它会让原本自由的三个旋转轴“锁死”一个自由度,导致姿态无法唯一描述,甚至引发数值计算崩溃。
一个真实的“卡住”场景
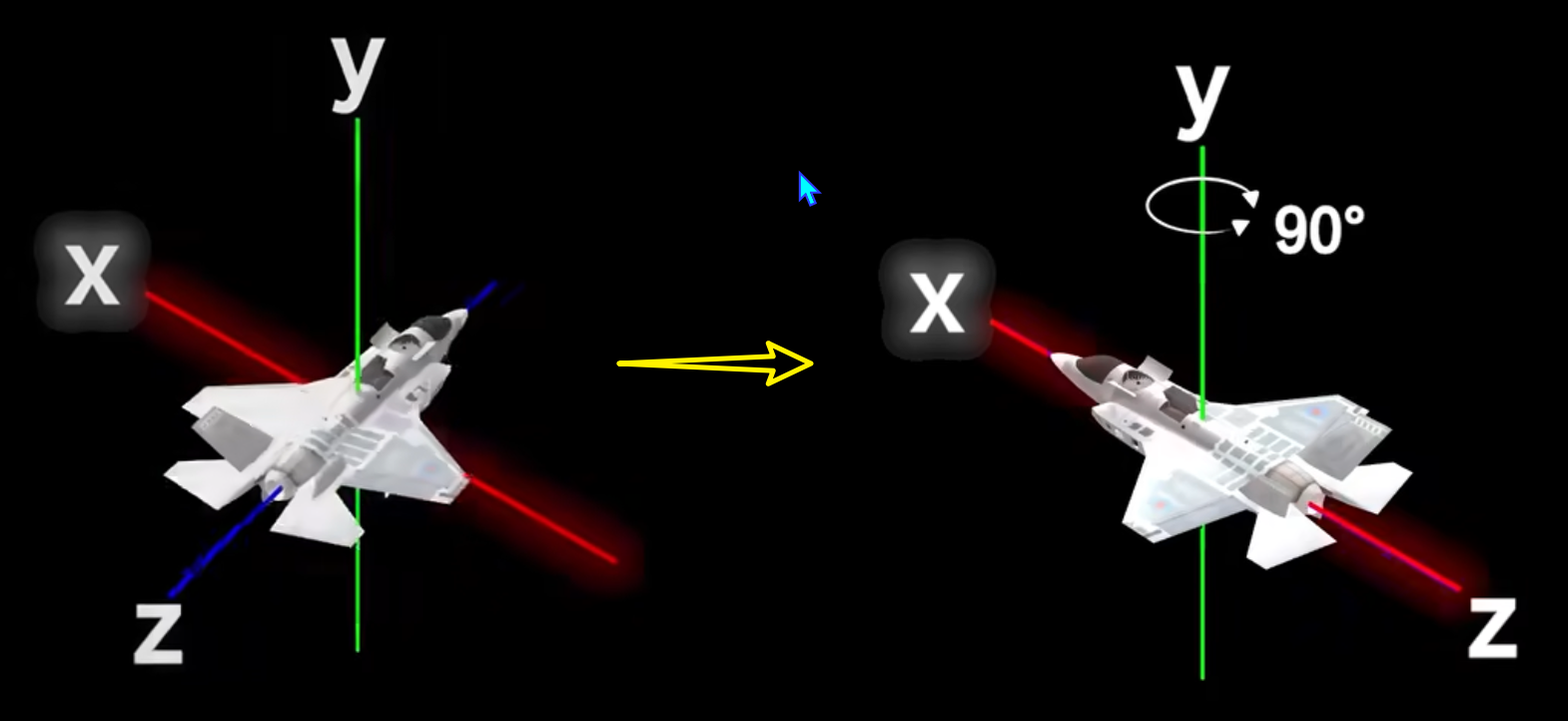
假设一架飞机的俯仰角(绕Y轴的Pitch)被调整到90度此时:
原本绕Z轴的偏航(Yaw)旋转轴(世界坐标系的Z轴),会和绕X轴的滚转(Roll)旋转轴(飞机自身的X轴)完全重合(都指向世界坐标系的X轴方向)。
这时,无论你怎么调整Yaw或Roll的角度,飞机的姿态都不会改变——比如“向左转”和“向左翻滚”会产生完全相同的效果。
当俯仰角为90度时,三个欧拉角中只有两个独立参数,原本的“三个自由度”退化为“两个自由度”,这就是万向锁的数学本质:旋转矩阵的奇异性。
万向锁的危害
姿态歧义:同一姿态可能对应多组欧拉角(比如θ=90°时,φ和ψ可以有无限多组合);
动画抖动:当动画插值经过万向锁点(如从θ=80°到θ=100°),姿态会突然“跳变”;
物理模拟崩溃:机器人控制或航天器姿态计算中,万向锁可能导致控制器失效(比如无法稳定姿态)。
二、四元数
为了彻底解决欧拉角的万向锁问题,四元数(Quaternion)应用而生。
四元数是用4分量超复数 q=w+xi+yj+zk(单位四元数,w2+x2+y2+z2=1)表示旋转,本质是“旋转轴+旋转角度”的数学封装。
公式:q=[cos(θ/2),usin(θ/2)](u为旋转轴单位向量,θ为旋转角)。
2. 四元数如何“消灭”万向锁?
万向锁的本质是欧拉角依赖固定轴的旋转顺序,导致中间轴旋转时破坏了轴的正交性。而四元数直接用“轴-角”表示旋转,不依赖任何外部坐标系,因此不会出现轴重合的问题。无论旋转角度多大(即使是180度),四元数始终能唯一表示姿态。
3. 四元数丝滑插值
在游戏或动画中,我们常需要让物体从一个姿态“平滑过渡”到另一个姿态(比如角色转身)。用欧拉角直接线性插值(Lerp)会导致“路径扭曲”(比如经过万向锁点时姿态突变),而四元数的球面线性插值(Slerp)可以沿着“最短旋转路径”平滑过渡,效果自然流畅。
举个例子:从“抬头45度”到“低头45度”,欧拉角插值可能会先“低头到-90度”再“回正”,而四元数Slerp会直接走“最短路径”(低头90度),动画效果更合理。
4. 四元数的“缺点”:反直觉
四元数的缺点也很明显:四个分量(w, x, y, z)没有直接的几何意义(不像欧拉角对应“抬头”“转身”),难以直接理解或手动输入。因此,它更适合作为“计算工具”存储在引擎内部,而不是让用户直接操作。
实战
这个演示创建了三个相同的飞机模型:
右侧橙色飞机:使用欧拉角进行旋转
左侧紫色飞机:使用四元数进行旋转
顶部绿色飞机:作为参考的简单旋转

欧拉角旋转(橙色飞机)
// 欧拉角旋转实现代码
eulerPlane.rotation.x = Math.sin(time) * Math.PI / 2;
eulerPlane.rotation.y = Math.cos(time) * Math.PI / 2;
eulerPlane.rotation.z = time;观察橙色飞机的运动时,会发现以下问题:
万向节死锁:当飞机进行复杂旋转时,会出现突然的抖动和不自然的运动
不连续性:在某些角度,飞机的运动会出现跳跃
旋转次序依赖:x、y、z轴的旋转顺序会影响最终结果
四元数旋转(紫色飞机)
// 四元数旋转实现代码
const quaternion = new THREE.Quaternion();
quaternion.setFromAxisAngle(
new THREE.Vector3(Math.sin(time), Math.cos(time), 1).normalize(),
0.05
);
quaternionPlane.quaternion.multiplyQuaternions(quaternion, quaternionPlane.quaternion);观察紫色飞机的运动特点:
平滑过渡:旋转过程中没有突然的跳跃或抖动
稳定性:即使在复杂的旋转组合中也能保持平滑
无万向节死锁:不会出现欧拉角中的万向节死锁问题
另外补充:
让飞机轨迹更加平滑,使用插值算法
const smoothPoints = (points: THREE.Vector3[]) => {
if (points.length < 2) return points;
const smoothed: THREE.Vector3[] = [];
for (let i = 0; i < points.length - 1; i++) {
const current = points[i];
const next = points[i + 1];
smoothed.push(current);
if (i < points.length - 2) {
const midPoint = new THREE.Vector3().addVectors(current, next).multiplyScalar(0.5);
smoothed.push(midPoint);
}
}
smoothed.push(points[points.length - 1]);
return smoothed;
};